Geometri telah lama menjadi cabang ilmu yang menarik, bukan hanya di kalangan ahli matematika tetapi juga bagi para pengamat seni dan arsitektur. Dalam kajian geometri, konsep sumbu simetri memainkan peran yang sangat penting. Sumbu simetri adalah garis imajiner yang membagi suatu bentuk menjadi dua bagian yang identik. Hal ini tidak hanya relevan dalam matematika tetapi juga memberikan wawasan yang mendalam tentang keseimbangan dan keindahan dalam desain. Pada artikel ini, kita akan membahas jumlah sumbu simetri pada sebuah bentuk yang spesifik dan menggali makna di baliknya.
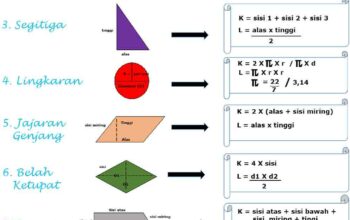
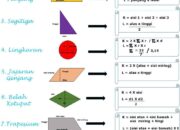
Ketika kita membahas sumbu simetri, kita sering dihadapkan pada berbagai bentuk geometri, mulai dari yang sederhana seperti segitiga hingga yang lebih kompleks seperti heksagon dan lingkaran. Masing-masing bentuk ini memiliki karakteristik unik yang menentukan banyaknya sumbu simetri. Mari kita eksplorasi lebih lanjut.
Mari kita mulai dengan mendefinisikan bentuk yang akan kita analisis. Gambar yang dimaksud mengandung beberapa elemen visual yang dapat dihitung dari perspektif simetri. Dengan pendekatan analitis, kita akan menelusuri langkah demi langkah untuk menemukan berapa banyak sumbu simetri yang ada pada gambar tersebut.
Pentingnya memahami sumbu simetri bukan hanya sekedar menghitung; detailnya berakar pada bagaimana objek tersebut berinteraksi dengan sumbu tersebut. Apakah objek akan tetap utuh jika dipantulkan melalui garis sumbu? Pertanyaan ini akan memandu kita dalam analisis ini.
Menggali Definisi dan Klasifikasi Sumbu Simetri
Sebelum melanjutkan, mari kita lakukan klasifikasi sumbu simetri berdasarkan bentuk geometri yang umum. Beberapa yang paling dikenal adalah:
1. **Sumbu Simetri Vertikal**: Garis ini membagi bentuk menjadi dua bagian yang merupakan cerminan dari satu sama lain secara vertikal. Contohnya adalah bentuk seperti segitiga sama kaki.
2. **Sumbu Simetri Horizontal**: Garis ini membagi bentuk secara horizontal. Sebuah persegi panjang, misalnya, memiliki dua sumbu simetri horizontal.
3. **Sumbu Simetri Diagonal**: Beberapa bentuk, seperti persegi, memiliki sumbu simetri diagonal yang juga membagi bentuk menjadi dua bagian yang identik.
4. **Sumbu Simetri Tak Terbatas**: Lingkaran adalah contoh sempurna dari bentuk yang memiliki sumbu simetri tak terbatas, ia dapat dipotong dari mana saja dan tetap simetris.
Penting untuk dicatat bahwa tidak semua bentuk memiliki sumbu simetri. Bentuk tidak simetris seperti jajargenjang yang tidak sama kaki akan memiliki sumbu simetri yang terbatas. Sekarang, mengacu kembali pada gambar yang kita analisis, kita harus mengidentifikasi kategori sumbu simetri yang relevan dengan bentuk tersebut.
Analisis Komprehensif Gambar Terpilih
Ketika kita meneliti bentuk dalam gambar, hal pertama yang harus dilakukan adalah mengidentifikasi kontur dan garis batas bentuk tersebut. Dalam hal ini, gambar representatif akan menampilkan beberapa karakteristik yang dapat diukur.
Kita mulai dengan mengamati titik pusat koordinat. Apakah gambar tersebut menunjukkan sentra yang memungkinkan pembagian dua sisi yang sama? Dari sini kita dapat sentuhan pertama untuk memahami berapa banyak sumbu simetri yang ada. Biasanya, maranggi yang komprehensif akan menunjukkan simetri dan keseimbangan.
Dalam konteks ini, dua pertanyaan mendasar muncul: Apakah bentuknya simetris secara vertikal, horizontal, atau mungkin diagonal? Atau, apakah bentuk tersebut memiliki lebih dari satu sumbu simetri? Ketiga kemungkinan ini akan kita teliti lebih dalam.
Setelah mengidentifikasi jenis sumbu, mari kita fokus pada kemampuan cetak biru. Kegiatan memvisualisasikan atau menggambar garis-garis sumbu simetri pada objek yang diamati dapat mengungkap sisi simetris yang mengendap dalam karakter bentuk itu sendiri. Hasil analisis dari gambar ini akan memberikan pemahaman yang lebih dalam mengenai struktur internal dan estetika objek.
Implikasi Sumbu Simetri dalam Desain dan Estetika
Sumbu simetri tidak hanya sekedar relevan dalam konteks matematika; mereka juga menjadi penting dalam desain dan estetika. Hal ini menyentuh ranah seni, arsitektur, dan bahkan biologi. Misalnya, dalam desain grafis, penggunaan sumbu simetri membantu menciptakan keseimbangan visual yang menarik.
Satu contoh ekstrem adalah seni Islam dan arsitektur yang sering menerapkan simetri untuk menciptakan persepsi ketenangan dan harmoni. Dalam hal ini, sumbu simetri bukan hanya secara matematis relevan, tetapi juga menjadi pusat dari filosofi dan pengalaman visual.
Di dunia flora dan fauna, banyak organisme memiliki sumbu simetri natu. Contohnya, koleksi kupu-kupu atau bunga yang menggunakan simetri radian untuk menjamin kelangsungan hidup dan daya tarik visual bagi pengunjung alaminya.
Dalam matematika, sumbu simetri membantu peneliti dalam memahami pola dan relasi dalam algoritma. Bagaimana hal ini berfungsi dalam perangkat pengenalan pola misalnya? Memahami sumbu simetri memungkinkan mereka untuk mengejar efisiensi dalam algoritma yang berfungsi dalam pengenalan pola dan pengolahan citra.
Secara keseluruhan, penting untuk menjelajahi multidimensi dari konsep sumbu simetri ini. Begitu banyak yang dapat dieksplorasi dari perspektif yang berbeda — matematis, estetis, bahkan biologis!
Untuk merangkum, dalam konteks gambar yang telah dianalisis, jumlah sumbu simetri akan sangat bergantung pada karakternya. Menggali lebih dalam bukan hanya menjawab pertanyaan sederhana semata, tetapi sekaligus membawa kita pada pemahaman yang lebih luas tentang keterhubungan dalam desain, alam, dan ilmu pengetahuan. Mengambil langkah lebih jauh dalam menganalisis dan memperdalam eksplorasi ini dapat menjadi kunci untuk menemukan simetri di dunia di sekitar kita. Manfaatkan kejanggalan dan pertanyaan yang berkembang untuk membawa kajian kita pada level pemahaman yang lebih tinggi.